Ильченко С.В., Елизарова И.В. Выбор параметров криптосистемы как фактор эффективности информационной безопасности
Ильченко С.В., Елизарова И.В. Выбор параметров криптосистемы как фактор эффективности информационной безопасности
Образец ссылки на эту статью: Ильченко С.В., Елизарова И.В. Выбор параметров криптосистемы как фактор эффективности информационной безопасности // Бизнес и дизайн ревю. 2019. № 4 (16). С. 8.
УДК 004.056; 658.027
ВЫБОР ПАРАМЕТРОВ КРИПТОСИСТЕМЫ КАК ФАКТОР ЭФФЕКТИВНОСТИ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ ОРГАНИЗАЦИИ
Ильченко Светлана Владимировна
НОЧУ ВО «Московский экономический институт», Москва, Россия (109390, Москва, ул. Артюхиной, д. 6, корп. 1), кандидат педагогических наук, доцент, strelec200763@mail.ru
Елизарова Ирина Владимировна
Институт прикладной математики и механики. Санкт-Петербургский государственный политехнический университет Петра Великого, Санкт-Петербург, Россия (195251, г. Санкт-Петербург, ул. Политехническая, д. 29), магистрант направления подготовки 10.04.01 «Информационная безопасность», irina.elizarova.vl@gmail.com, +7-910-531-96-37.
Аннотация. Криптографические системы защиты информации играют большую роль в современной жизни, в частности, в процессе управления организацией. На сегодняшний день интерес к проблеме защиты информации очень высок, информация — один из самых важных ресурсов любого предприятия. Ее своевременное получение, эффективное использование, надлежащее хранение и безопасная передача играют определяющую роль в деятельности компании, сказываются на ее прибыльности и развитии. В статье изложены основные принципы функционирования криптосистемы PFLASH. Сформулированы требования к параметрам криптосистемы при использовании нечётной характеристики специального вида . Выявлены зависимости между параметрами, показана возможность использования системы в связи с большим набором параметров. Показано поведение системы на различных параметрах, выбранных в соответствии с выведенными требованиями. Результаты, полученные в ходе работы, позволяют улучшить временные характеристики криптографической схемы, уменьшить размер открытого ключа и увеличить количество доступных безопасных параметров.
Ключевые слова: постквантовая криптография; многомерная криптография; схемы «большого поля»; PFLASH; поле нечётной характеристики.
CHOICE OF PARAMETERS OF THE CRYPTOSYSTEM AS A FACTOR OF THE EFFECTIVENESS OF THE INFORMATION SECURITY OF THE ORGANIZATION
Ilchenko Svetlana Vladimirovna
NOCU VO «Moscow Economic Institute», Moscow, Russia (109390, Moscow, Artyukhin St., 6, building 1), candidate of pedagogical sciences, associate Professor, strelec200763@mail.ru.
Elizarova Irina Vladimirovna
Institute of Applied Mathematics and Mechanics. Peter the Great St. Petersburg State Polytechnical University, St. Petersburg, Russia (195251, St. Petersburg, 29 Politekhnicheskaya St., 29), undergraduate in the direction of training 10.04.01 "Information Security", irina.elizarova.vl@gmail.com, +7-910-531-96-37.
Abstract. Cryptographic information protection systems play a large role in modern life, in particular, in the process of managing an organization. Today, interest in the problem of information protection is very high, and this is not surprising, because information is one of the most important resources of any enterprise. Its timely receipt, efficient use, proper storage and safe transfer play a decisive role in the company’s activities, affect its profitability and development. The article outlines the basic principles of the functioning of the cryptosystem PFLASH. The requirements are formulated for the parameters of the cryptosystem using an odd characteristic of a special kind q = 2 ^ 8 + 1. The dependencies between the parameters are revealed, the possibility of using the system in connection with a large set of parameters is shown. The behavior of the system on various parameters selected in accordance with the derived requirements is shown. The results obtained during the work allow to improve the temporal characteristics of the cryptographic scheme, reduce the size of the public key and increase the number of available secure parameters.
Key words: post-quantum cryptography; multivariate cryptography; big field schemes; PFLASH; odd-characteristic fields.
Введение
Успех любой современной компании и ее развитие в условиях острой конкуренции в большой степени зависят от применения информационных технологий, и, следовательно, от степени обеспечения информационной безопасности. Почти каждое предприятие располагает различными видами информации, представляющими интерес для злоумышленников. Прежде всего, это коммерческие данные, информация, являющаяся интеллектуальной собственностью предприятия и конфиденциальные данные.
Цель исследования – разработать криптосистемы и предложить соответствующие параметры для защиты информации в коммерческих организациях.
Методы исследования
При разработке темы использовались методы теории надежности, методы оптимизации, системный анализ.
Результаты исследования и их обсуждение
Информационная безопасность – это комплекс организационных, технических и технологических мер по защите информации от неавторизованного доступа, разрушения, модификации, раскрытия и задержек в доступе.
В настоящее время ведутся активные разработки квантовых вычислительных устройств. Так компания IBM уже предоставляет возможность использования Qiskit – открытой программной платформы для так называемого квантового программирования, а также использования квантовых схем при помощи облачной платформы IBM Quantum Experience.
В связи с этим возникает необходимость разработки новых криптографических алгоритмов, безопасность которых должна основываться на NP-полных задачах даже в условиях широкого распространения квантовых вычислений. Такие алгоритмы получили название постквантовых. Одним из направлений постквантовой криптографии является многомерная криптография с открытым ключом (Multivariate Public Key Cryptography, MPKC), где односторонняя «trap-door» функция принимает форму многомерного полиномиального отображения над конечным полем. А именно, открытый ключ обычно задается набором квадратичных полиномов:
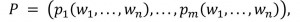
где каждый является (обычно квадратичным) нелинейным полиномом от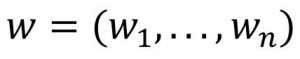
с коэффициентами из конечного поля. Вычисление значений этих полиномов для заданных значений соответствует либо процедуре шифрования, либо процедуре проверки.
Обращение многомерного квадратичного отображения эквивалентно решению системы квадратичных уравнений над конечным полем или задаче MQ, которая является NP-трудной [2].
Модификация «минус» удаляет R многочленов из открытого ключа. Таким образом, композиция этого минус-преобразования с аффинным преобразованием S имеет коранг r.
Следует отметить, что изучение научным сообществом этих криптосистем, и, в частности, PFLASH было ограничено использованием полей чётной характеристики. Предложенные параметры, обеспечивающие безопасность криптосистемы, в своём большинстве являются эмпирическими или выявленными экспериментально. Таким образом, был сделан вывод о целесообразности использования нечётной характеристики специального вида на примере .
Криптосистема с предложенными параметрами может использоваться организацией для решения проблемы недостаточного обеспечения безопасности путём формирования и проверки подписей передаваемых сообщений, поскольку только структурные особенности схемы не обеспечивают стойкость к существующим атакам.
На рисунке 1 приведена общая схема функционирования PFLASH – формирования и проверки подписи. Здесь – изоморфизм -векторного пространства , – хэш-образ подписываемого сообщения размерности , – сформированная подпись размерности .
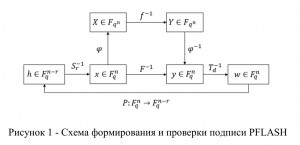
Фактически работу криптосистемы можно разделить на три этапа. Первый этап – генерация ключей. На нём производится выбор секретных отображений , выбирается степень центрального отображения . Вторым этапом является формирование подписи на закрытом ключе. Согласно
Третий этап – проверка подписи. Проверка осуществляется путем вычисления значений системы многочленов, составляющих открытый ключ. Элементы проверяемой подписи рассматриваются как значения неизвестных. На выходе – (n-r) значений, которые сравниваются с хэш-образом подписанного сообщения. Подпись считается верной при положительном результате сравнения и неверной в обратном случае.
Генерация открытого ключа согласно [8] может осуществляться двумя способами – интерполяцией полиномов и методом прямого обращения. Многопараметрические криптосистемы имеют обширную историю криптоанализа. Было разработано несколько методов, которые показывают, что структуру легко обратимого центрального отображения скрыть достаточно трудно. Эти методы можно сгруппировать в две категории [6] – структурные атаки (ранговые атаки, атака по инвариантному подпространству, дифференциальные атаки, атака по структуре расширенного поля, обратное преобразование низкой степени и др.) и общие атаки (например, методы, основанные на базисах Грёбнера, включая алгоритм Бухбергера, его усовершенствования (такие как F4 и F5), алгоритм XL и алгоритм Чжуан-Цзы).
Для получения хотя бы одного удовлетворяющего значения , необходимо, чтобы этому удовлетворял, по крайней мере, первый интервал. Таким образом, появляется ограничение на степень расширения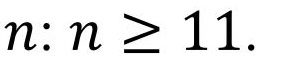
Отдельно для этого параметра конкретные рекомендации не даются. Однако от зависит размер ключевой пары, подписи, а также длительность и сложность их формирования и проверки подписи. В связи с этим должно быть не слишком большим. Кроме того, следует отметить, что помимо всего прочего должно выполняться условие
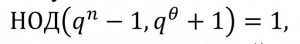
которое автоматически выполняется при чётной характеристике и ранее не упоминалось. Однако выбранная для исследования характеристика нечётная – q=257. Соответственно, при любых выбранных показателях и ,
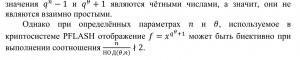
Таким образом, при заданных ограничениях были рассмотрены возможные параметры для криптосистемы исходя из различных значений степени расширения поля, т.е. параметра . График зависимости количества наборов безопасных параметров от представлен на рисунке 2.
При реализации криптосистемы на скрытых отображениях полей нечётной характеристики q=257 PFLASH использовалась свободно распространяемая математическая система SageMath 8.7, язык программирования Python. Проведён эксперимент с изменением степени расширения и, соответственно, количеством удаляемых из открытого ключа полиномов.
Рассматривалось три значения показателя – минимально возможное, среднее и максимальное. Ниже на рисунках 3-5 приведены результаты исследования.
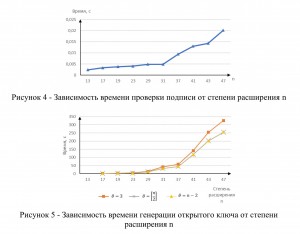
Также была исследована зависимость размера открытого ключа от степени расширения n, приведено сравнение (рисунок 6) с размерами ключа, получаемого при использовании рекомендованных в [3] параметров. Данные криптосистемы на этих параметрах, используемые для графика, также приведены в [3]. При реализации открытый ключ хранится в качестве не набора полиномов, а только их коэффициентов.
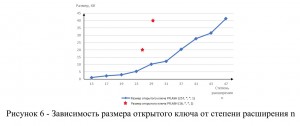
Результаты, полученные при тестировании системы, позволяют считать использование характеристики q=257 не только возможным, но и эффективным, поскольку время формирования и проверки подписи, генерации открытого ключа и его размер являются приемлемыми для использования криптосистемы PFLASH.
Кроме того, поскольку была выбрана нечётная характеристика специального вида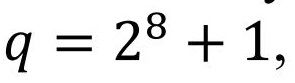
, данная реализация криптосистемы была также перенесена на Arduino Nano, процессор ATMega328 для проверки того, возможна ли в принципе реализация PFLASH с характеристикой q=257 на маломощных устройствах. Использовалась интегрированная среда разработки Arduino IDE 1.6.5. Так время проверки подписи зависит от следующим образом.
Таблица 1 - Время проверки подписи на Arduino Nano
Реализация на маломощных устройствах возможна. Однако для успешного функционирования системы требуется использование специальных алгоритмов на этапе разработки. Так криптосхема становится ориентированной на конкретное устройство, улучшая временные характеристики функционирования.
При рассмотрении криптосистемы на скрытых отображениях полей характеристики q=257 было выявлено, что с увеличением степени расширения увеличивается мощность безопасного пространства ключей. При практически минимальном значении количество возможных центральных отображений f равно 4. В то время как при увеличении характеристики всего в два раза до n=26, количество безопасных отображений возрастает до 12, т.е. в три раза. Это гарантирует широкие возможности использования данной схемы.
равным 1, однако для нечётной характеристики и условии простого это требование обусловлено только эффективностью вычислений, а не безопасностью, как это происходит для чётной характеристики.
Однако в ходе работы также были выявлены ограничения на параметр 0, характеризующий центральное отображение схемы f. Количество таких возможных θ – зависит от степени расширения как N=n-9.
Выводы
Результаты экспериментального исследования позволяют сделать вывод о том, что использование нечётных характеристик возможно. При реализации с использованием специальных алгоритмов схема PFLASH осуществляет достаточно быстрый процесс формирования и проверки подписи, генерации открытого ключа.
Таким образом, криптография дает средства для защиты информации, и поэтому она является частью эффективной деятельности по обеспечению безопасности информации.
Список литературы
References
Рецензент:
Васяев А.П. – кандидат экономических наук, доцент кафедры менеджмента, НОЧУ ВО «Московский экономический институт».
Работа поступила в редакцию: 10.10.2019 г.
УДК 004.056; 658.027
ВЫБОР ПАРАМЕТРОВ КРИПТОСИСТЕМЫ КАК ФАКТОР ЭФФЕКТИВНОСТИ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ ОРГАНИЗАЦИИ
Ильченко Светлана Владимировна
НОЧУ ВО «Московский экономический институт», Москва, Россия (109390, Москва, ул. Артюхиной, д. 6, корп. 1), кандидат педагогических наук, доцент, strelec200763@mail.ru
Елизарова Ирина Владимировна
Институт прикладной математики и механики. Санкт-Петербургский государственный политехнический университет Петра Великого, Санкт-Петербург, Россия (195251, г. Санкт-Петербург, ул. Политехническая, д. 29), магистрант направления подготовки 10.04.01 «Информационная безопасность», irina.elizarova.vl@gmail.com, +7-910-531-96-37.
Аннотация. Криптографические системы защиты информации играют большую роль в современной жизни, в частности, в процессе управления организацией. На сегодняшний день интерес к проблеме защиты информации очень высок, информация — один из самых важных ресурсов любого предприятия. Ее своевременное получение, эффективное использование, надлежащее хранение и безопасная передача играют определяющую роль в деятельности компании, сказываются на ее прибыльности и развитии. В статье изложены основные принципы функционирования криптосистемы PFLASH. Сформулированы требования к параметрам криптосистемы при использовании нечётной характеристики специального вида . Выявлены зависимости между параметрами, показана возможность использования системы в связи с большим набором параметров. Показано поведение системы на различных параметрах, выбранных в соответствии с выведенными требованиями. Результаты, полученные в ходе работы, позволяют улучшить временные характеристики криптографической схемы, уменьшить размер открытого ключа и увеличить количество доступных безопасных параметров.
Ключевые слова: постквантовая криптография; многомерная криптография; схемы «большого поля»; PFLASH; поле нечётной характеристики.
CHOICE OF PARAMETERS OF THE CRYPTOSYSTEM AS A FACTOR OF THE EFFECTIVENESS OF THE INFORMATION SECURITY OF THE ORGANIZATION
Ilchenko Svetlana Vladimirovna
NOCU VO «Moscow Economic Institute», Moscow, Russia (109390, Moscow, Artyukhin St., 6, building 1), candidate of pedagogical sciences, associate Professor, strelec200763@mail.ru.
Elizarova Irina Vladimirovna
Institute of Applied Mathematics and Mechanics. Peter the Great St. Petersburg State Polytechnical University, St. Petersburg, Russia (195251, St. Petersburg, 29 Politekhnicheskaya St., 29), undergraduate in the direction of training 10.04.01 "Information Security", irina.elizarova.vl@gmail.com, +7-910-531-96-37.
Abstract. Cryptographic information protection systems play a large role in modern life, in particular, in the process of managing an organization. Today, interest in the problem of information protection is very high, and this is not surprising, because information is one of the most important resources of any enterprise. Its timely receipt, efficient use, proper storage and safe transfer play a decisive role in the company’s activities, affect its profitability and development. The article outlines the basic principles of the functioning of the cryptosystem PFLASH. The requirements are formulated for the parameters of the cryptosystem using an odd characteristic of a special kind q = 2 ^ 8 + 1. The dependencies between the parameters are revealed, the possibility of using the system in connection with a large set of parameters is shown. The behavior of the system on various parameters selected in accordance with the derived requirements is shown. The results obtained during the work allow to improve the temporal characteristics of the cryptographic scheme, reduce the size of the public key and increase the number of available secure parameters.
Key words: post-quantum cryptography; multivariate cryptography; big field schemes; PFLASH; odd-characteristic fields.
Введение
Успех любой современной компании и ее развитие в условиях острой конкуренции в большой степени зависят от применения информационных технологий, и, следовательно, от степени обеспечения информационной безопасности. Почти каждое предприятие располагает различными видами информации, представляющими интерес для злоумышленников. Прежде всего, это коммерческие данные, информация, являющаяся интеллектуальной собственностью предприятия и конфиденциальные данные.
Цель исследования – разработать криптосистемы и предложить соответствующие параметры для защиты информации в коммерческих организациях.
Методы исследования
При разработке темы использовались методы теории надежности, методы оптимизации, системный анализ.
Результаты исследования и их обсуждение
Информационная безопасность – это комплекс организационных, технических и технологических мер по защите информации от неавторизованного доступа, разрушения, модификации, раскрытия и задержек в доступе.
В настоящее время ведутся активные разработки квантовых вычислительных устройств. Так компания IBM уже предоставляет возможность использования Qiskit – открытой программной платформы для так называемого квантового программирования, а также использования квантовых схем при помощи облачной платформы IBM Quantum Experience.
В связи с этим возникает необходимость разработки новых криптографических алгоритмов, безопасность которых должна основываться на NP-полных задачах даже в условиях широкого распространения квантовых вычислений. Такие алгоритмы получили название постквантовых. Одним из направлений постквантовой криптографии является многомерная криптография с открытым ключом (Multivariate Public Key Cryptography, MPKC), где односторонняя «trap-door» функция принимает форму многомерного полиномиального отображения над конечным полем. А именно, открытый ключ обычно задается набором квадратичных полиномов:
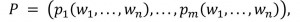
где каждый является (обычно квадратичным) нелинейным полиномом от
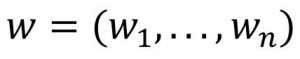с коэффициентами из конечного поля. Вычисление значений этих полиномов для заданных значений соответствует либо процедуре шифрования, либо процедуре проверки.Обращение многомерного квадратичного отображения эквивалентно решению системы квадратичных уравнений над конечным полем или задаче MQ, которая является NP-трудной [2].
Модификация «минус» удаляет R многочленов из открытого ключа. Таким образом, композиция этого минус-преобразования с аффинным преобразованием S имеет коранг r.
Следует отметить, что изучение научным сообществом этих криптосистем, и, в частности, PFLASH было ограничено использованием полей чётной характеристики. Предложенные параметры, обеспечивающие безопасность криптосистемы, в своём большинстве являются эмпирическими или выявленными экспериментально. Таким образом, был сделан вывод о целесообразности использования нечётной характеристики специального вида на примере .
Криптосистема с предложенными параметрами может использоваться организацией для решения проблемы недостаточного обеспечения безопасности путём формирования и проверки подписей передаваемых сообщений, поскольку только структурные особенности схемы не обеспечивают стойкость к существующим атакам.
На рисунке 1 приведена общая схема функционирования PFLASH – формирования и проверки подписи. Здесь – изоморфизм -векторного пространства , – хэш-образ подписываемого сообщения размерности , – сформированная подпись размерности .
Фактически работу криптосистемы можно разделить на три этапа. Первый этап – генерация ключей. На нём производится выбор секретных отображений , выбирается степень центрального отображения . Вторым этапом является формирование подписи на закрытом ключе. Согласно
Третий этап – проверка подписи. Проверка осуществляется путем вычисления значений системы многочленов, составляющих открытый ключ. Элементы проверяемой подписи рассматриваются как значения неизвестных. На выходе – (n-r) значений, которые сравниваются с хэш-образом подписанного сообщения. Подпись считается верной при положительном результате сравнения и неверной в обратном случае.
Генерация открытого ключа согласно [8] может осуществляться двумя способами – интерполяцией полиномов и методом прямого обращения. Многопараметрические криптосистемы имеют обширную историю криптоанализа. Было разработано несколько методов, которые показывают, что структуру легко обратимого центрального отображения скрыть достаточно трудно. Эти методы можно сгруппировать в две категории [6] – структурные атаки (ранговые атаки, атака по инвариантному подпространству, дифференциальные атаки, атака по структуре расширенного поля, обратное преобразование низкой степени и др.) и общие атаки (например, методы, основанные на базисах Грёбнера, включая алгоритм Бухбергера, его усовершенствования (такие как F4 и F5), алгоритм XL и алгоритм Чжуан-Цзы).
Для получения хотя бы одного удовлетворяющего значения , необходимо, чтобы этому удовлетворял, по крайней мере, первый интервал. Таким образом, появляется ограничение на степень расширения
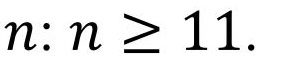
Отдельно для этого параметра конкретные рекомендации не даются. Однако от зависит размер ключевой пары, подписи, а также длительность и сложность их формирования и проверки подписи. В связи с этим должно быть не слишком большим. Кроме того, следует отметить, что помимо всего прочего должно выполняться условие
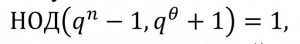
которое автоматически выполняется при чётной характеристике и ранее не упоминалось. Однако выбранная для исследования характеристика нечётная – q=257. Соответственно, при любых выбранных показателях и ,
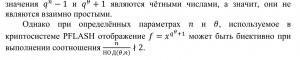
Таким образом, при заданных ограничениях были рассмотрены возможные параметры для криптосистемы исходя из различных значений степени расширения поля, т.е. параметра . График зависимости количества наборов безопасных параметров от представлен на рисунке 2.
При реализации криптосистемы на скрытых отображениях полей нечётной характеристики q=257 PFLASH использовалась свободно распространяемая математическая система SageMath 8.7, язык программирования Python. Проведён эксперимент с изменением степени расширения и, соответственно, количеством удаляемых из открытого ключа полиномов.
Рассматривалось три значения показателя – минимально возможное, среднее и максимальное. Ниже на рисунках 3-5 приведены результаты исследования.
Также была исследована зависимость размера открытого ключа от степени расширения n, приведено сравнение (рисунок 6) с размерами ключа, получаемого при использовании рекомендованных в [3] параметров. Данные криптосистемы на этих параметрах, используемые для графика, также приведены в [3]. При реализации открытый ключ хранится в качестве не набора полиномов, а только их коэффициентов.
Результаты, полученные при тестировании системы, позволяют считать использование характеристики q=257 не только возможным, но и эффективным, поскольку время формирования и проверки подписи, генерации открытого ключа и его размер являются приемлемыми для использования криптосистемы PFLASH.
Кроме того, поскольку была выбрана нечётная характеристика специального вида
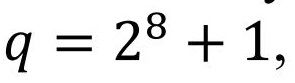, данная реализация криптосистемы была также перенесена на Arduino Nano, процессор ATMega328 для проверки того, возможна ли в принципе реализация PFLASH с характеристикой q=257 на маломощных устройствах. Использовалась интегрированная среда разработки Arduino IDE 1.6.5. Так время проверки подписи зависит от следующим образом.Таблица 1 - Время проверки подписи на Arduino Nano
Реализация на маломощных устройствах возможна. Однако для успешного функционирования системы требуется использование специальных алгоритмов на этапе разработки. Так криптосхема становится ориентированной на конкретное устройство, улучшая временные характеристики функционирования.
При рассмотрении криптосистемы на скрытых отображениях полей характеристики q=257 было выявлено, что с увеличением степени расширения увеличивается мощность безопасного пространства ключей. При практически минимальном значении количество возможных центральных отображений f равно 4. В то время как при увеличении характеристики всего в два раза до n=26, количество безопасных отображений возрастает до 12, т.е. в три раза. Это гарантирует широкие возможности использования данной схемы.
равным 1, однако для нечётной характеристики и условии простого это требование обусловлено только эффективностью вычислений, а не безопасностью, как это происходит для чётной характеристики.
Однако в ходе работы также были выявлены ограничения на параметр 0, характеризующий центральное отображение схемы f. Количество таких возможных θ – зависит от степени расширения как N=n-9.
Выводы
Результаты экспериментального исследования позволяют сделать вывод о том, что использование нечётных характеристик возможно. При реализации с использованием специальных алгоритмов схема PFLASH осуществляет достаточно быстрый процесс формирования и проверки подписи, генерации открытого ключа.
Таким образом, криптография дает средства для защиты информации, и поэтому она является частью эффективной деятельности по обеспечению безопасности информации.
Список литературы
- Cartor R., Smith-Tone D. An Updated Security Analysis of PFLASH - Post-Quantum Cryptography. PQCrypto 2017. Lecture Notes in Computer Science. 2017. Vol. 10346. pp. 241–254.
- Chen M., Ding J., Petzoldt A., Tao C., Yang B. Design Principles for HFEv- based Multivariate Signature Schemes - Advances in Cryptology - ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science. 2015. Vol. 9452. pp. 311-334.
- Chen M., Smith-Tone D., Yang B. PFLASH – Secure Asymmetric Signatures on Smartcards [Электронный ресурс] https://ws680.nist.gov – URL: https://ws680.nist.gov/publication/get_pdf.cfm?pub_id=926103. (дата обращения 19.10.2019).
- Courtois, N., Goubin, L., Patarin, J. Improved algorithms for isomorphisms of polynomials - Advances in Cryptology — EUROCRYPT'98. EUROCRYPT 1998. Lecture Notes in Computer Science. 1998. Vol. 1403. pp. 184–200. [Электронный ресурс] https://pdfs.semanticscholar.org. URL: https://pdfs.semanticscholar.org/95f6/05929be4ec7db07f8838fae1c3a08b58dc8a.pdf. – (дата обращения 18.10.2019).
- Ding J., Kleinjung T. Degree of regularity for HFE- Post-Quantum Cryptography. PQCrypto 2013. Lecture Notes in Computer Science. 2013. Vol. 7932. pp. 52–66.
- Ding J., Yang B.-Y. Multivariate Public Key Cryptography - Post-Quantum Cryptography. – 2016. – P. 193–241. [Электронный ресурс] http://www.moscito.org. URL: http://www.moscito.org/by-publ/recent/pqc.pdf. (дата обращения 17.10.2019).
- Matsumoto T., Imai H. Public Quadratic Polynominal-Tuples for Efficient Signature-Verification and Message-Encryption - Lecture Notes in Computer Science on Advances in Cryptology-EUROCRYPT'88. 1988. pp. 419–453.
- Wolf C. Hidden Field Equations (HFE) – Variations and Attacks [Электронный ресурс] http://www.christopher-wolf.de. URL: http://www.christopher-wolf.de/dpl/thesis_hfe_wolf.pdf. (дата обращения 19.10.2019).
References
- Cartor R., Smith-Tone D. An Updated Security Analysis of PFLASH - Post-Quantum Cryptography. PQCrypto 2017. Lecture Notes in Computer Science. 2017. Vol. 10346. pp. 241–254.
- Chen M., Ding J., Petzoldt A., Tao C., Yang B. Design Principles for HFEv- based Multivariate Signature Schemes - Advances in Cryptology - ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science. 2015. Vol. 9452. pp. 311-334.
- Chen M., Smith-Tone D., Yang B. PFLASH – Secure Asymmetric Signatures on Smartcards [Elektronnyy resurs] https://ws680.nist.gov – URL: https://ws680.nist.gov/publication/get_pdf.cfm?pub_id=926103. (data obrashheniya 19.10.2019).
- Courtois, N., Goubin, L., Patarin, J. Improved algorithms for isomorphisms of polynomials - Advances in Cryptology — EUROCRYPT'98. EUROCRYPT 1998. Lecture Notes in Computer Science. 1998. Vol. 1403. pp. 184–200. [Elektronnyy resurs] https://pdfs.semanticscholar.org. URL: https://pdfs.semanticscholar.org/95f6/05929be4ec7db07f8838fae1c3a08b58dc8a.pdf. – (data obrashheniya 18.10.2019).
- Ding J., Kleinjung T. Degree of regularity for HFE- Post-Quantum Cryptography. PQCrypto 2013. Lecture Notes in Computer Science. 2013. Vol. 7932. pp. 52–66.
- Ding J., Yang B.-Y. Multivariate Public Key Cryptography - Post-Quantum Cryptography. – 2016. – P. 193–241. [Elektronnyy resurs] http://www.moscito.org. URL: http://www.moscito.org/by-publ/recent/pqc.pdf. (data obrashheniya 17.10.2019).
- Matsumoto T., Imai H. Public Quadratic Polynominal-Tuples for Efficient Signature-Verification and Message-Encryption - Lecture Notes in Computer Science on Advances in Cryptology-EUROCRYPT'88. 1988. pp. 419–453.
- Wolf C. Hidden Field Equations (HFE) – Variations and Attacks [Elektronnyy resurs] http://www.christopher-wolf.de – URL: http://www.christopher-wolf.de/dpl/thesis_hfe_wolf.pdf. (data obrashheniya 19.10.2019).
Рецензент:
Васяев А.П. – кандидат экономических наук, доцент кафедры менеджмента, НОЧУ ВО «Московский экономический институт».
Работа поступила в редакцию: 10.10.2019 г.
